与えられた微分方程式の挙動を見るには微分方程式を解けばよいが,一般的に解析解を求めることは難しい.
その際に役立つのが数値シミュレーションである.
初期値やパラメータ値をかえることで,様々なシナリオに応じた結果・挙動をin silicoで見ることが可能である.
Rではdesolveやsimecolといったパッケージが用意されており,簡単にモデルの実装が可能である.
一方で,これらのパッケージの中身を理解せずに使うと,数値計算の段階でエラーが起きても対処できない.
ここでは,数値計算法の導出方法を学ぶ.
まず,次の形の初期値問題を考える.
\begin{equation} \frac{dx}{dt} = f(t,x), \quad x(t_0) = x_0 . \end{equation}
解\(x(t)=x(t,t_0,x_0)\)は\(x(t):[t_0,T]\rightarrow \mathbb{R}\)であり,\(p+1\)解微分可能であるとする.
すると\(x(t_n)\)は\(t_n \in [t_0,T]\)のまわりでTaylor展開することができ,
\begin{equation}
x(t_n) = x(t_{n-1}) + \Delta_n \frac{dx}{dt}(t_{n-1}) + \frac{1}{2}\Delta_n^2 \frac{d^2x}{dt^2}(t_{n-1}) + \cdots +
\frac{1}{p!} \Delta_n^p \frac{d^px}{dt^p}(t_{n-1}) + \frac{1}{(p+1)!}\Delta_n^{p+1} \frac{d^{p+1}x}{dt^{p+1}}(\theta_{n-1})
\end{equation}
ただし,\(\Delta_n = t_n – t_{n-1}\)かつ\(\theta_n \in [t_{n-1},t_n] \subset [t_0,T]\)とする.
微分作用素\(D\)として
$$D g(t,x) := \frac{\partial g}{\partial t}(t,x) + f(t,x)\frac{\partial g}{\partial t}(t,x)$$
を導入し,\(g\)にchain ruleを使うと,
$$\frac{dg}{dt}(t,x(t)) = \frac{\partial g}{\partial t}(t,x(t)) + \frac{\partial g}{\partial x}(t,x(t))f(t,x(t)) = Dg(t,x(t))$$
ただし,\(dx/dt=f(t,x(t))\)を途中で使った.
作用素\(D\)を使うと\(x(t)\)の導関数は
$$\frac{d^j x}{dt^j} = D^{j-1} f(t,x(t)), \quad j=1,2,\dots$$
と書くことができる.
上式を\(D\)を使って書き直すと,
\begin{equation}
x(t_n) = x(t_{n-1}) + \sum_{j=1}^p \frac{1}{j!} D^{j-1} f(t_{n-1},x(t_{n-1})) \Delta_n^j + \frac{1}{(j+1)!}D^p f(\theta_{n-1},x(\theta_{n-1})) \Delta_n^{p+1}
\end{equation}
が得られる.
この式で最後の項を除外すると\(p\)次のTaylor法を作ることができる.
\begin{equation}
x_n = x_{n-1} + \sum_{j=1}^p \frac{1}{j!} D^{j-1} f(t_{n-1},x_{n-1}) \Delta_n^j
\end{equation}
ただし,\(x_n\)は\(x(t)\)の\(t=t_n\)における近似値である.
最後に除外した項が実際の解との誤差ということになる.
つまり,局所離散化誤差(local discretization error)は,
$$L_n := |x(t_n,t_{n-1},x(t_{n-1})) – x_n|$$
で与えられ,
$$ L_n \leq \frac{1}{(j+1)!} \Delta_n^{p+1} |D^p f(\theta_{n-1},x(\theta_{n-1},t_{n-1},x(t_{n-1})))| \sim \cal{O}(\Delta_n^{p+1})$$
となる.
一般的に係数\(D^{h-1}f(t_{n-1},x(t_{n-1}))\)を計算するのは非常に難しく,実際に実装されるのは少ない.
どちらかというと,他の数値計算法を作るのに使われたり,誤差の評価のために使われることが多い.
実際にどのくらい近似値がかわってくるかを指数関数を用いて調べてみた.
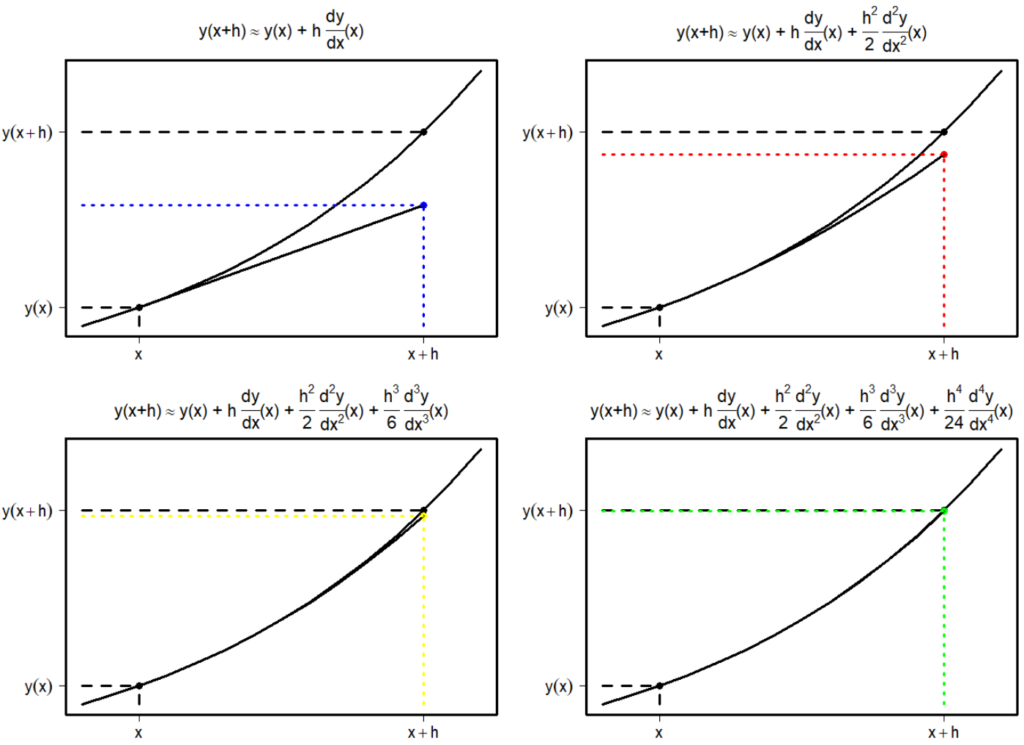
上のfigureを作ったコードはこちら.指数関数の導関数を与え,そこに数値を入れていった.
プログラム自体はほぼ一緒なので,Euler法によるもののみ紹介:
xaxis_value=c(1,2)
xaxis_label=c(expression(x),expression(x+h))
yaxis_value=c(exp(1),exp(2))
yaxis_label=c(expression(y(x)),expression(y(x+h)))
plot(x,exp(x),type='l',lwd=3,xlab='',ylab='',xlim=c(0.8,2.2),ylim=c(exp(0.8),exp(2.2)),xaxt='n',yaxt='n')
title(main=expression(paste("y(x+h)"%~~%"y(x) + h ",frac(dy,dx),"(x)")),cex.main=1.1)
axis(1,xaxis_value,xaxis_label)
axis(2,yaxis_value,yaxis_label,las=2)
points(1,exp(1),pch=16,cex=1.5)
points(2,exp(2),pch=16,cex=1.5)
segments(1,exp(0.8),1,exp(1),lty=2)
segments(0.8,exp(1),1,exp(1),lty=2)
segments(0.8,exp(2),2,exp(2),lty=2)
points(2,2*exp(1),pch=16,cex=1.5,col='blue')
segments(1,exp(1),2,2*exp(1))
segments(2,exp(0.8),2,2*exp(1),lty=3,col='blue')
segments(0.8,2*exp(1),2,2*exp(1),lty=3,col='blue')